Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 151, pp. 1-13.
A singular third-order 3-point boundary-value problem with
nonpositive Green's function
Alex P. Palamides, Anastasia N. Veloni
Abstract:
We find a Green's function for the singular third-order
three-point BVP

where
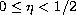 . Then we apply the classical
Krasnosel'skii's fixed point theorem for finding solutions
in a cone.
Although this problem Green's function is not positive, the
obtained solution is still positive and increasing.
Our techniques rely on a combination of a fixed point theorem and
the properties of the corresponding vector field.
. Then we apply the classical
Krasnosel'skii's fixed point theorem for finding solutions
in a cone.
Although this problem Green's function is not positive, the
obtained solution is still positive and increasing.
Our techniques rely on a combination of a fixed point theorem and
the properties of the corresponding vector field.
Submitted October 11, 2007. Published November 13, 2007.
Math Subject Classifications: 34B15, 34B18, 34B10, 34B16.
Key Words: Three-point singular boundary-value problem;
fixed point in cones; third-order differential equation;
positive solution; Green's function; vector field.
Show me the
PDF file (238 KB),
TEX file, and other files for this article.
 |
Alex P. Palamides
Department of Telecommunications Science and Technology
University of Peloponnese
Karaiskaki Str., 22100 Tripolis, Greece
email: palamid@uop.gr |
|---|
 |
Anastasia N. Veloni
Technological Education Institute of Piraeus
Department of Electronic Computer Systems
P. Ralli Ave. & Thivon Ave. 250
Aigaleo 12244, Athens, Greece
email: aveloni@teipir.gr
|
|---|
Return to the EJDE web page

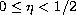 . Then we apply the classical
Krasnosel'skii's fixed point theorem for finding solutions
in a cone.
Although this problem Green's function is not positive, the
obtained solution is still positive and increasing.
Our techniques rely on a combination of a fixed point theorem and
the properties of the corresponding vector field.
. Then we apply the classical
Krasnosel'skii's fixed point theorem for finding solutions
in a cone.
Although this problem Green's function is not positive, the
obtained solution is still positive and increasing.
Our techniques rely on a combination of a fixed point theorem and
the properties of the corresponding vector field.

