Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 145, pp. 1-18.
Regularization for evolution equations in Hilbert spaces
involving monotone operators via the semi-flows method
George L. Karakostas, Konstantina G. Palaska
Abstract:
In a Hilbert space
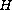 consider the equation
consider the equation
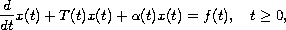
where the family of operators
 ,
,
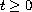 converges in a
certain sense to a monotone operator
converges in a
certain sense to a monotone operator
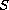 ,
the function
,
the function
 vanishes at infinity and the function
vanishes at infinity and the function
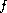 converges to a point
converges to a point
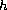 .
In this paper we provide sufficient conditions that
guarantee the fact that full limiting functions of any solution of
the equation are points of the orthogonality set
.
In this paper we provide sufficient conditions that
guarantee the fact that full limiting functions of any solution of
the equation are points of the orthogonality set
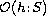 of
of
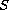 at
at
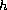 ,
namely the set of all
,
namely the set of all
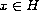 such that
such that
 ,
for all
,
for all
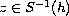 .
If the set
.
If the set
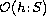 is a singleton, then the original
solution converges to a solution of the algebraic equation
is a singleton, then the original
solution converges to a solution of the algebraic equation
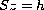 .
Our problem is faced by using the semi-flow theory and it extends
to various directions the works [1,12].
.
Our problem is faced by using the semi-flow theory and it extends
to various directions the works [1,12].
Submitted September 10, 2007. Published October 30, 2007.
Math Subject Classifications: 39B42, 34D45, 47H05, 47A52, 70G60.
Key Words: Hilbert spaces; monotone operators; regularization; evolutions;
semi-flows; limiting equations; full limiting functions;
convergence.
An addendum was posted on September 15, 2008. The authors correct some misprints
and clarify a uniform boundedness. Please see the last page of this manuscript.
Show me the
PDF file (282 KB),
TEX file, and other files for this article.
 |
George L. Karakostas
Department of Mathematics
University of Ioannina
451 10 Ioannina, Greece
email: gkarako@uoi.gr |
|---|
 |
Konstantina G. Palaska
Department of Mathematics
University of Ioannina
451 10 Ioannina, Greece
|
|---|
Return to the EJDE web page
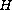 consider the equation
consider the equation
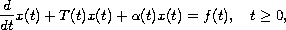
 ,
,
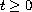 converges in a
certain sense to a monotone operator
converges in a
certain sense to a monotone operator
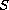 ,
the function
,
the function
 vanishes at infinity and the function
vanishes at infinity and the function
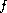 converges to a point
converges to a point
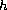 .
In this paper we provide sufficient conditions that
guarantee the fact that full limiting functions of any solution of
the equation are points of the orthogonality set
.
In this paper we provide sufficient conditions that
guarantee the fact that full limiting functions of any solution of
the equation are points of the orthogonality set
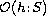 of
of
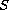 at
at
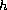 ,
namely the set of all
,
namely the set of all
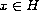 such that
such that
 ,
for all
,
for all
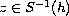 .
If the set
.
If the set
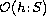 is a singleton, then the original
solution converges to a solution of the algebraic equation
is a singleton, then the original
solution converges to a solution of the algebraic equation
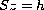 .
Our problem is faced by using the semi-flow theory and it extends
to various directions the works [1,12].
.
Our problem is faced by using the semi-flow theory and it extends
to various directions the works [1,12].

