The first order nonlinear ordinary differential equation
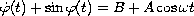 ,
which is commonly used as a simple model of an overdamped
Josephson junction in superconductors is investigated.
Its general solution is obtained in the case known as
phase-lock where all but one solution converge to a
common `essentially periodic' attractor.
The general solution is represented in explicit form
in terms of the Floquet solution of a double confluent Heun equation.
In turn, the latter
solution is represented through the Laurent series
which defines an analytic function on the Riemann sphere with
punctured poles.
The series coefficients are given in terms of infinite products
of
,
which is commonly used as a simple model of an overdamped
Josephson junction in superconductors is investigated.
Its general solution is obtained in the case known as
phase-lock where all but one solution converge to a
common `essentially periodic' attractor.
The general solution is represented in explicit form
in terms of the Floquet solution of a double confluent Heun equation.
In turn, the latter
solution is represented through the Laurent series
which defines an analytic function on the Riemann sphere with
punctured poles.
The series coefficients are given in terms of infinite products
of
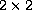 matrices with a single zero element.
The closed form of the phase-lock condition is obtained and
represented as the condition for existence of a real root of
a transcendental function.
The efficient phase-lock criterion is conjectured, and
its plausibility is confirmed in numerical tests.
matrices with a single zero element.
The closed form of the phase-lock condition is obtained and
represented as the condition for existence of a real root of
a transcendental function.
The efficient phase-lock criterion is conjectured, and
its plausibility is confirmed in numerical tests.
