Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 130, pp. 1-20.
Variation of constants formula for functional parabolic
partial differential equations
Alexander Carrasco, Hugo Leiva
Abstract:
This paper presents a variation of constants formula for
the system of functional parabolic partial differential equations
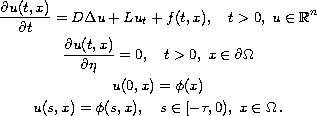
Here
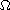 is a bounded domain in
is a bounded domain in
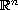 ,
the
,
the
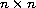 matrix
matrix
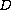 is block diagonal with semi-simple eigenvalues
having non negative real part, the operator
is block diagonal with semi-simple eigenvalues
having non negative real part, the operator
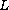 is bounded and linear,
the delay in time is bounded, and the standard
notation
is bounded and linear,
the delay in time is bounded, and the standard
notation
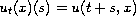 is used.
is used.
Submitted July 2, 2007. Published October 5, 2007.
Math Subject Classifications: 34G10, 35B40.
Key Words: Functional partial parabolic equations;
variation of constants formula; strongly continuous semigroups.
Show me the
PDF file (267 KB),
TEX file, and other files for this article.
 |
Alexander Carrasco
Universidad Centroccidental Lisandro Alvarado
Decanato de Ciencias, Departamento de Matemática
Barquisimeto 3001, Venezuela
email: acarrasco@ucla.edu.ve
|
|---|
 |
Hugo Leiva
Universidad de los Andes
Department of Mathemátics
Mérida 5101, Venezuela
email: hleiva@ula.ve
|
|---|
Return to the EJDE web page
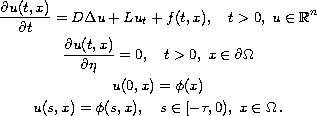
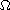 is a bounded domain in
is a bounded domain in
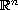 ,
the
,
the
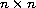 matrix
matrix
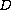 is block diagonal with semi-simple eigenvalues
having non negative real part, the operator
is block diagonal with semi-simple eigenvalues
having non negative real part, the operator
 is bounded and linear,
the delay in time is bounded, and the standard
notation
is bounded and linear,
the delay in time is bounded, and the standard
notation
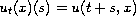 is used.
is used.

