Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 13, pp. 1-10.
Positive periodic solutions of neutral
logistic equations with distributed delays
Yongkun Li, Guoqiao Wang, Huimei Wang
Abstract:
Using a fixed point theorem of strict-set-contraction,
we establish criteria for the existence of positive periodic
solutions for the periodic neutral logistic equation,
with distributed delays,
![$$
x'(t)= x(t)\Big[a(t)-\sum_{i=1}^n a_i(t)\int_{-T_i}^0 x(t+\theta)\,
d\mu_i(\theta)- \sum_{j=1}^m b_j(t)
\int_{-\hat{T}_j}^0 x'(t+\theta)\,d\nu_j(\theta)\Big],
$$](gifs/aa.gif)
where the coefficients
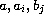 are continuous and periodic functions,
with the same period. The values
are continuous and periodic functions,
with the same period. The values
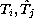 are positive,
and the functions
are positive,
and the functions
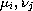 are nondecreasing with
are nondecreasing with
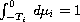 and
and
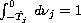 .
.
Submitted July 14, 2006. Published January 8, 2007.
Math Subject Classifications: 34K13, 34K40.
Key Words: Positive periodic solution; neutral delay logistic equation;
strict-set-contraction.
Show me the
PDF file (222K),
TEX file, and other files for this article.
Yongkun Li
Department of Mathematics,
Yunnan University
Kunming, Yunnan 650091, China
email: yklie@ynu.edu.cn
|
Guoqiao Wang
Department of Mathematics,
Yunnan University
Kunming, Yunnan 650091, China
email:wgq81@126.com |
Huimei Wang
Department of Mathematics,
Yunnan University
Kunming, Yunnan 650091, China
email: wanghmei@163.com |
Return to the EJDE web page
![$$
x'(t)= x(t)\Big[a(t)-\sum_{i=1}^n a_i(t)\int_{-T_i}^0 x(t+\theta)\,
d\mu_i(\theta)- \sum_{j=1}^m b_j(t)
\int_{-\hat{T}_j}^0 x'(t+\theta)\,d\nu_j(\theta)\Big],
$$](gifs/aa.gif)
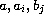 are continuous and periodic functions,
with the same period. The values
are continuous and periodic functions,
with the same period. The values
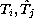 are positive,
and the functions
are positive,
and the functions
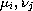 are nondecreasing with
are nondecreasing with
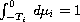 and
and
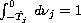 .
.