The spatially periodic Kuramoto-Sivashinsky equation (pKS)
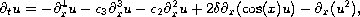
with
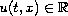 ,
,
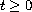 ,
,
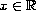 ,
is a model problem for inclined film flow
over wavy bottoms and other spatially periodic systems
with a long wave instability.
For given
,
is a model problem for inclined film flow
over wavy bottoms and other spatially periodic systems
with a long wave instability.
For given
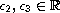 and small
and small
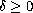 it has
a one dimensional family of spatially periodic stationary solutions
it has
a one dimensional family of spatially periodic stationary solutions
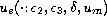 ,
parameterized by the mass
,
parameterized by the mass
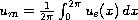 .
Depending on the parameters these stationary solutions
can be linearly stable or unstable.
We show that in the stable case localized perturbations decay with a
polynomial rate and in a universal nonlinear self-similar way: the limiting
profile is determined by a Burgers equation in Bloch wave space.
We also discuss linearly unstable
.
Depending on the parameters these stationary solutions
can be linearly stable or unstable.
We show that in the stable case localized perturbations decay with a
polynomial rate and in a universal nonlinear self-similar way: the limiting
profile is determined by a Burgers equation in Bloch wave space.
We also discuss linearly unstable
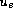 ,
in which case we approximate
the pKS by a constant coefficient KS-equation. The analysis is based on
Bloch wave transform and renormalization group methods.
,
in which case we approximate
the pKS by a constant coefficient KS-equation. The analysis is based on
Bloch wave transform and renormalization group methods.

