Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 112, pp. 1-7.
Multiple positive solutions for nonlinear third-order
three-point boundary-value problems
Li-Jun Guo, Jian-Ping Sun, Ya-Hong Zhao
Abstract:
This paper concerns the nonlinear third-order three-point
boundary-value problem
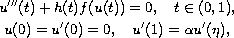
where
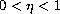 and
and
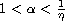 . First,
we establish the existence of at least three positive
solutions by using the well-known Leggett-Williams fixed point theorem.
And then, we prove the existence of at least
. First,
we establish the existence of at least three positive
solutions by using the well-known Leggett-Williams fixed point theorem.
And then, we prove the existence of at least
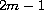 positive
solutions for arbitrary positive integer
positive
solutions for arbitrary positive integer
 .
.
Submitted April 18, 2007. Published August 18, 2007.
Math Subject Classifications: 34B10, 34B18.
Key Words: Third-order boundary value problem; positive solution;
three-point boundary value problem; existence; cone; fixed point.
Show me the
PDF file (184 KB),
TEX file, and other files for this article.
 |
Li-Jun Guo
Department of Applied Mathematics
Lanzhou University of Technology
Lanzhou, Gansu, 730050, China
email: school520@lut.cn
|
|---|
 |
Jian-Ping Sun
Department of Applied Mathematics
Lanzhou University of Technology
Lanzhou, Gansu, 730050, China
email: jpsun@lut.cn
|
|---|
 |
Ya-Hong Zhao
Department of Applied Mathematics
Lanzhou University of Technology
Lanzhou, Gansu, 730050, China
email: zhaoyahong88@sina.com
|
|---|
Return to the EJDE web page
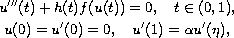
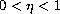 and
and
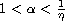 . First,
we establish the existence of at least three positive
solutions by using the well-known Leggett-Williams fixed point theorem.
And then, we prove the existence of at least
. First,
we establish the existence of at least three positive
solutions by using the well-known Leggett-Williams fixed point theorem.
And then, we prove the existence of at least
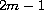 positive
solutions for arbitrary positive integer
positive
solutions for arbitrary positive integer
 .
.


