We prove the existence of infinitely many solutions to a semilinear Dirichlet boundary value problem in a ball for a nonlinearity
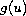 that grows subcritically for
that grows subcritically for
 positive and supercritically for
positive and supercritically for
 negative.
negative.
Alfonso Castro, John Kwon, Chee Meng Tan
Abstract:
We prove the existence of infinitely many solutions to a
semilinear Dirichlet boundary value problem in a ball
for a nonlinearity
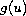 that grows subcritically for
that grows subcritically for
 positive and supercritically for
positive and supercritically for
 negative.
negative.
Submitted February 4, 2007. Published August 14, 2007.
Math Subject Classifications: 35J65, 34B16.
Key Words: Sub-super critical; radial solutions;
nonlinear elliptic equation; Pohozaev identity.
Show me the PDF file (216 KB), TEX file, and other files for this article.
 |
Alfonso Castro Departament of Mathematics, Harvey Mudd College Claremont, CA 91711, USA email: castro@math.hmc.edu |
|---|---|
| John Kwon Departament of Mathematics, Harvey Mudd College Claremont, CA 91711, USA email: kwonjy@math.uci.edu | |
| Chee Meng Tan Departament of Mathematics, Harvey Mudd College Claremont, CA 91711, USA email: ctan@hmc.edu |
Return to the EJDE web page