Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 109, pp. 1-11.
Initial-boundary value problems for nonlinear pseudoparabolic
equations in a critical case
Elena I. Kaikina
Abstract:
We study nonlinear pseudoparabolic equations, on the half-line
in a critical case,
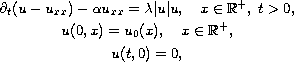
where
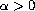 ,
,
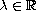 .
The aim of this paper is to prove the existence of global solutions
to the initial-boundary value problem and to find the main term
of the asymptotic representation of solutions.
.
The aim of this paper is to prove the existence of global solutions
to the initial-boundary value problem and to find the main term
of the asymptotic representation of solutions.
Submitted March 22, 2007. Published August 7, 2007.
Math Subject Classifications: 35Q35
Key Words: Dissipative nonlinear evolution equation; Sobolev equation;
large time asymptotic behavior.
Show me the
PDF file (332 KB),
TEX file, and other files for this article.
 |
Elena I. Kaikina
Instituto de Matemáticas
Universidad Nacional Aut&ocute;noma de México
Campus Morelia, AP 61-3 (Xangari)
Morelia CP 58089, Michoacán, Mexico
email: ekaikina@matmor.unam.mx
|
|---|
Return to the EJDE web page
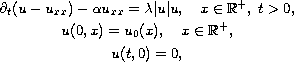
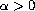 ,
,
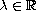 .
The aim of this paper is to prove the existence of global solutions
to the initial-boundary value problem and to find the main term
of the asymptotic representation of solutions.
.
The aim of this paper is to prove the existence of global solutions
to the initial-boundary value problem and to find the main term
of the asymptotic representation of solutions.
