Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 108, pp. 1-11.
Relations between the small functions and the solutions of
certain second-order differential equations
Huifang Liu, Zhiqiang Mao
Abstract:
In this paper, we investigate the relations between the small
functions and the solutions, first, second derivatives, and differential
polynomial of the solutions to the differential equation
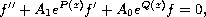
where
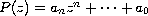 ,
,
 are polynomials
with degree
are polynomials
with degree
 (
(
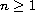 ),
),
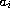 ,
,
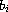 (
(
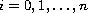 ),
),
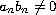 are complex constants,
are complex constants,
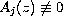 (
(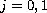 )
are entire functions with
)
are entire functions with
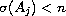 .
.
Submitted February 12, 2007. Published August 7, 2007.
Math Subject Classifications: 34M10.
Key Words: Entire function; exponent of convergence of the zero-sequence.
Show me the
PDF file (239 KB),
TEX file, and other files for this article.
 |
Huifang Liu
School of Mathematics, South China Normal University
Guangzhou 510631, China.
Institute of Mathematics and Informatics
Jiangxi Normal University, Nanchang 330027, China
email: liuhuifang73@sina.com
|
|---|
 |
Zhiqiang Mao
School of Mathematics, South China Normal University
Guangzhou 510631, China.
Depatment of Mathematics
Jiangxi Science and Teachers college, Nanchang 330013, China
email: maozhiqiang1@sina.com
|
|---|
ReturZhiqiang Mao\newline
School of Mathematics, South China Normal University,
Guangzhou 510631, China. \newline
Depatment of Mathematics, Jiangxi Science and Teachers college,
Nanchang 330013, China}
\email{maozhiqiang1@sina.comn to the EJDE web page
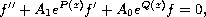
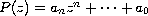 ,
,
 are polynomials
with degree
are polynomials
with degree
 (
(
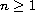 ),
),
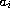 ,
,
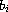 (
(
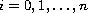 ),
),
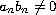 are complex constants,
are complex constants,
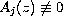 (
(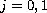 )
are entire functions with
)
are entire functions with
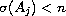 .
.

