Electron. J. Diff. Eqns.,
Vol. 2007(2007), No. 10, pp. 1-11.
Oscillation criteria for second-order neutral differential
equations with distributed deviating arguments
Gaihua Gui, Zhiting Xu
Abstract:
Using a class of test functions
 defined by Sun
[13] and a generalized Riccati technique, we establish some new
oscillation criteria for the second-order neutral differential
equation with distributed deviating argument
defined by Sun
[13] and a generalized Riccati technique, we establish some new
oscillation criteria for the second-order neutral differential
equation with distributed deviating argument
![$$
(r(t)\psi(x(t))Z'(t))'+\int^b_a
q(t,\xi)f[x(g(t,\xi))]d\sigma(\xi)=0,\quad t\geq t_0,
$$](gifs/ab.gif)
where
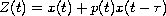 .
The obtained results are different
from most known ones and can be applied to many cases which are
not covered by existing results.
.
The obtained results are different
from most known ones and can be applied to many cases which are
not covered by existing results.
Submitted July 28, 2006. Published January 2, 2007.
Math Subject Classifications: 34K11, 34C10, 34K40.
Key Words: Oscillation; neutral differential equation; second order;
distributed deviating argument; Riccati technique.
Show me the
PDF file (242K),
TEX file, and other files for this article.
 |
Gaihua Gui
School of Mathematical Sciences
South China Normal University
Guangzhou, 510631, China
email: 1981hgg@163.com |
|---|
 |
Zhiting Xu
School of Mathematical Sciences
South China Normal University
Guangzhou, 510631, China
email: xztxhyyj@pub.guangzhou.gd.cn
|
|---|
Return to the EJDE web page
 defined by Sun
[13] and a generalized Riccati technique, we establish some new
oscillation criteria for the second-order neutral differential
equation with distributed deviating argument
defined by Sun
[13] and a generalized Riccati technique, we establish some new
oscillation criteria for the second-order neutral differential
equation with distributed deviating argument
![$$
(r(t)\psi(x(t))Z'(t))'+\int^b_a
q(t,\xi)f[x(g(t,\xi))]d\sigma(\xi)=0,\quad t\geq t_0,
$$](gifs/ab.gif)
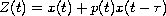 .
The obtained results are different
from most known ones and can be applied to many cases which are
not covered by existing results.
.
The obtained results are different
from most known ones and can be applied to many cases which are
not covered by existing results.

