In this paper, we consider the higher order neutral nonlinear difference equation
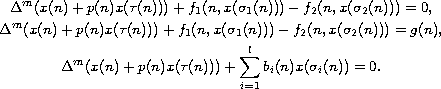
We obtain sufficient conditions for the existence of non-oscillatory solutions.
Qiaoluan Li, Haiyan Liang, Wenlei Dong, Zhenguo Zhang
Abstract:
In this paper, we consider the higher order neutral nonlinear
difference equation
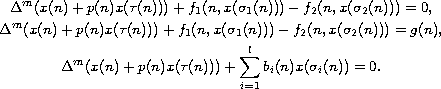
We obtain sufficient conditions for the existence of non-oscillatory
solutions.
Submitted April 30, 2006. Published January 2, 2007.
Math Subject Classifications: 39A05, 39A10.
Key Words: Nonoscillatory; existence; neutral equation.
Show me the PDF file (199K), TEX file, and other files for this article.
 |
Qiaoluan Li College of Mathematics and Information Science Hebei Normal University Shijiazhuang, 050016, China mail: qll71125@163.com |
|---|---|
 |
Haiyan Liang College of Mathematics and Information Science Hebei Normal University Shijiazhuang, 050016, China |
| Wenlei Dong College of Mathematics and Information Science Hebei Normal University Shijiazhuang, 050016, China | |
 |
Zhenguo Zhang College of Mathematics and Information Science Hebei Normal University, Shijiazhuang, 050016, China Information College, Zhejiang Ocean University Zhoushan, Zhejiang, 316000, China email: Zhangzhg@mail.hebtu.edu.cn |
Return to the EJDE web page