We prove that the Cauchy problem of the Schrodinger-Korteweg-deVries (NLS-KdV) system for periodic functions is globally well-posed for initial data in the energy space
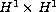 .
More precisely, we
show that the non-resonant NLS-KdV system is globally well-posed for
initial data in
.
More precisely, we
show that the non-resonant NLS-KdV system is globally well-posed for
initial data in
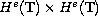 with s>11/13 and the resonant NLS-KdV system is globally well-posed
with s>8/9.
The strategy is to apply the I-method used by Colliander, Keel,
Staffilani, Takaoka and Tao. By doing this, we improve the
results by Arbieto, Corcho and Matheus concerning the global
well-posedness of NLS-KdV systems.
with s>11/13 and the resonant NLS-KdV system is globally well-posed
with s>8/9.
The strategy is to apply the I-method used by Colliander, Keel,
Staffilani, Takaoka and Tao. By doing this, we improve the
results by Arbieto, Corcho and Matheus concerning the global
well-posedness of NLS-KdV systems.
