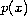 -Laplace operator
-Laplace operator
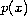 -Laplace operator
-Laplace operator
Maria-Magdalena Boureanu
Abstract:
In this paper we study an elliptic equation involving the
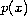 -Laplace
operator on the whole space
-Laplace
operator on the whole space
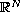 .
For that equation we prove the existence of a nontrivial
weak solution using as main argument the mountain pass
theorem of Ambrosetti and Rabinowitz.
.
For that equation we prove the existence of a nontrivial
weak solution using as main argument the mountain pass
theorem of Ambrosetti and Rabinowitz.
Submitted June 6, 2006. Published August 22, 2006.
Math Subject Classifications: 35D05, 35J60, 35J70, 58E05, 76A02.
Key Words: p(x)-Laplace operator; Sobolev space with variable exponent;
mountain pass theorem; weak solution.
A corrigendum was posted on December 1, 2006. The author restated Hypothesis (F2) and the proof of Theroem 3.2. See the last page of this manuscript.
Show me the PDF file (210K), TEX file, and other files for this article.
 |
Maria-Magdalena Boureanu Department of Mathematics University of Craiova 200585 Craiova, Romania email: mmboureanu@yahoo.com |
|---|
Return to the EJDE web page