Electron. J. Diff. Eqns.,
Vol. 2006(2006), No. 93, pp. 1-8.
Asymptotic behaviour of the solution for the singular
Lane-Emden-Fowler equation with nonlinear convection terms
Zhijun Zhang
Abstract:
We show the exact asymptotic behaviour near the
boundary for the classical solution to the Dirichler
problem
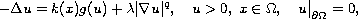
where
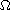 is a bounded domain with smooth boundary in
is a bounded domain with smooth boundary in
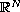 .
We use the Karamata regular varying theory, a perturbed argument,
and constructing comparison functions.
.
We use the Karamata regular varying theory, a perturbed argument,
and constructing comparison functions.
Submitted December 23, 2005. Published August 18, 2006.
Math Subject Classifications: 35J65, 35B05, 35O75, 35R05.
Key Words: Semilinear elliptic equations; Dirichlet problem; singularity;
nonlinear convection terms; Karamata regular variation theory;
unique solution; exact asymptotic behaviour.
Show me the
PDF file (232K),
TEX file, and other files for this article.
 |
Zhijun Zhang
Department of Mathematics and Informational Science
Yantai University, Yantai, Shandong, 264005, China
email: zhangzj@ytu.edu.cn |
|---|
Return to the EJDE web page
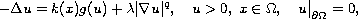
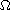 is a bounded domain with smooth boundary in
is a bounded domain with smooth boundary in
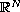 .
We use the Karamata regular varying theory, a perturbed argument,
and constructing comparison functions.
.
We use the Karamata regular varying theory, a perturbed argument,
and constructing comparison functions.
