Electron. J. Diff. Eqns.,
Vol. 2006(2006), No. 89, pp. 1-16.
Nonlinear pseudodifferential equations on a half-line
with large initial data
Rosa E. Cardiel, Elena I. Kaikina
Abstract:
We study the initial-boundary value problem for nonlinear pseudodifferential
equations, on a half-line,
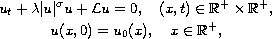
where
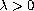 and pseudodifferential operator
and pseudodifferential operator
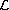 is defined by
the inverse Laplace transform. The aim of this paper is to prove the global
existence of solutions and to find the main term of the asymptotic
representation in the case of the large initial data.
is defined by
the inverse Laplace transform. The aim of this paper is to prove the global
existence of solutions and to find the main term of the asymptotic
representation in the case of the large initial data.
Submitted February 10, 2006. Published August 9, 2006.
Math Subject Classifications: 35Q35, 35B40.
Key Words: Pseudodifferential operator; large data; asymptotic behavior.
Show me the
PDF file (257K),
TEX file, and other files for this article.
 |
Rosa E. Cardiel
Instituto de Matemáticas UNAM
(Campus Cuernavaca), Av. Universidad s/n
col. Lomas de Chamilpa, Cuernavaca, Morelos, Mexico
email: rosy@matcuer.unam.mx |
|---|
 |
Elena I. Kaikina
Instituto de Matemáticas UNAM
Campus Morelia, AP 61-3 (Xangari)
Morelia CP 58089, Michoacán, Mexico
email: ekaikina@matmor.unam.mx |
|---|
Return to the EJDE web page
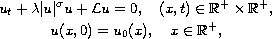
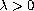 and pseudodifferential operator
and pseudodifferential operator
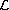 is defined by
the inverse Laplace transform. The aim of this paper is to prove the global
existence of solutions and to find the main term of the asymptotic
representation in the case of the large initial data.
is defined by
the inverse Laplace transform. The aim of this paper is to prove the global
existence of solutions and to find the main term of the asymptotic
representation in the case of the large initial data.

