Electron. J. Diff. Eqns., Vol. 2006(2006), No. 77, pp. 1-10.

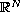
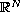
Strong global attractor for a quasilinear nonlocal wave equation on $\mathbb{R}^N$

Perikles G. Papadopoulos, Nikolaos M. Stavrakakis

Abstract:
We study the long time behavior of solutions to the nonlocal quasilinear dissipative wave equation
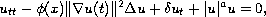
$$ u_{tt}-\phi (x)\|\nabla u(t)\|^{2}\Delta u+\delta u_{t}+|u|^{a}u=0, $$
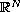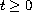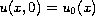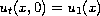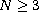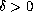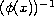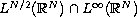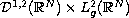in $\mathbb{R}^N$, $t \geq 0$, with initial conditions $ u(x,0) = u_0 (x)$ and $u_t(x,0) = u_1(x)$. We consider the case $N \geq 3$, $\delta> 0$, and $(\phi (x))^{-1}$ a positive function in $L^{N/2}(\mathbb{R}^N)\cap L^{\infty}(\mathbb{R}^N )$. The existence of a global attractor is proved in the strong topology of the space $\mathcal{D}^{1,2}(\mathbb{R}^N) \times L^{2}_{g}(\mathbb{R}^N)$.

Submitted May 10, 2006. Published Juy 12, 2006.
Math Subject Classifications: 35A07, 35B30, 35B40, 35B45, 35L15, 35L70, 35L80.
Key Words: Quasilinear hyperbolic equations; Kirchhoff strings; global attractor; unbounded domains; generalized Sobolev spaces; weighted 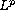$L^p$ spaces.

Show me the PDF file (252K), TEX file, and other files for this article.

Perikles G. Papadopoulos
Department of Mathematics, National Technical University
Zografou Campus, 157 80 Athens, Greece
email: perispap@math.ntua.gr
Nikolaos M. Stavrakakis
Department of Mathematics, National Technical University
Zografou Campus, 157 80 Athens, Greece
email: nikolas@central.ntua.gr

Return to the EJDE web page