Electron. J. Diff. Eqns., Vol. 2006(2006), No. 69, pp. 1-10.

Existence of weak solutions for nonlinear elliptic systems on $\mathbb{R}^N$

Eada A. El-Zahrani, Hassan M. Serag

Abstract:
In this paper, we consider the nonlinear elliptic system
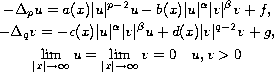
$$\displaylines{ -\Delta_pu=a(x)|u|^{p-2}u-b(x)|u|^\alpha|v|^\beta v+f,\cr -\Delta_qv=-c(x)|u|^\alpha |v|^\beta u + d(x) |v|^{q-2}v +g ,\cr \lim_{|x|\to\infty}u=\lim_{|x|\to\infty}v=0\quad u,v>0 }$$
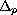on a bounded and unbounded domains of $\mathbb{R}^N$, where $\Delta_p$ denotes the p-Laplacian. The existence of weak solutions for these systems is proved using the theory of monotone operators

Submitted February 9, 2006. Published July 6, 2006.
Math Subject Classifications: 35B45, 35J55.
Key Words: Weak solutions; nonlinear elliptic systems; p-Laplacian; monotone operators.

Show me the PDF file (226K), TEX file, and other files for this article.

  Eada A. El-Zahrani
Mathematics Department, Faculty of Science for Girls
Dammam, P. O. Box 838, Pincode 31113, Saudi Arabia
Hassan M. Serag
Mathematics Department
Faculty of Science, Al-Azhar University
Nasr City (11884), Cairo, Egypt
email: serraghm@yahoo.com

Return to the EJDE web page