We study the existence of positive solutions for the boundary-value problem of the singular higher-order functional differential equation
![$$\displaylines{
(L y^{(n-2)})(t)+h(t)f(t, y_t)=0, \quad \hbox{for } t \in [0, 1], \cr
y^{(i)}(0) = 0, \quad 0 \leq i \leq n - 3, \cr
\alpha y^{(n-2)}(t)-\beta y^{(n-1)} (t)=\eta (t),
\quad \hbox{for } t \in [- \tau, 0],\cr
\gamma y^{(n-2)}(t) + \delta y^{(n-1)}(t) = \xi (t),
\quad \hbox{for } t \in [1, 1 + a],
}$$](gifs/aa.gif)
where
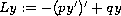 ,
,
![$p \in C([0, 1],(0, + \infty))$](gifs/ac.gif) ,
and
,
and
![$q \in C([0, 1], [0, + \infty))$](gifs/ad.gif) . Our main tool is the fixed
point theorem on a cone.
. Our main tool is the fixed
point theorem on a cone.
Chuanzhi Bai, Qing Yang, Jing Ge
Abstract:
We study the existence of positive solutions for the
boundary-value problem of the singular higher-order functional
differential equation
![$$\displaylines{
(L y^{(n-2)})(t)+h(t)f(t, y_t)=0, \quad \hbox{for } t \in [0, 1], \cr
y^{(i)}(0) = 0, \quad 0 \leq i \leq n - 3, \cr
\alpha y^{(n-2)}(t)-\beta y^{(n-1)} (t)=\eta (t),
\quad \hbox{for } t \in [- \tau, 0],\cr
\gamma y^{(n-2)}(t) + \delta y^{(n-1)}(t) = \xi (t),
\quad \hbox{for } t \in [1, 1 + a],
}$$](gifs/aa.gif)
where
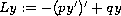 ,
,
![$p \in C([0, 1],(0, + \infty))$](gifs/ac.gif) ,
and
,
and
![$q \in C([0, 1], [0, + \infty))$](gifs/ad.gif) . Our main tool is the fixed
point theorem on a cone.
. Our main tool is the fixed
point theorem on a cone.
Submitted April 21, 2006. Published July 6, 2006.
Math Subject Classifications: 34K10, 34B16.
Key Words: Boundary value problem; higher-order;
positive solution; functional differential equation;
fixed point.
Show me the PDF file (241K), TEX file, and other files for this article.
 |
Chuanzhi Bai Department of Mathematics, Huaiyin Teachers College Huaian, Jiangsi 223001, China; and Department of Mathematics, Nanjing University Nanjing 210093, China email: czbai8@sohu.com |
|---|---|
 |
Qing Yang Department of Mathematics, Huaiyin Teachers College Huaian, Jiangsi 223001, China email: yangqing3511115@163.com |
 |
Jing Ge Department of Mathematics, Huaiyin Teachers College Huaian, Jiangsi 223001, China email: gejing0512@163.com |
Return to the EJDE web page