Electron. J. Diff. Eqns., Vol. 2006(2006), No. 63, pp. 1-13.
Existence of solutions for some nonlinear elliptic equations
Aomar Anane, Omar Chakrone, Mohammed Chehabi
Abstract:
In this paper, we study the existence of solutions to the following
nonlinear elliptic problem in a bounded subset
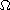 of
of
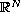 :
:
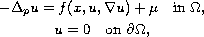
where
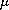 is a Radon measure on
is a Radon measure on
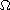 which is zero on
sets of
which is zero on
sets of
 -capacity zero,
-capacity zero,
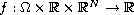 is a Caratheodory function that satisfies certain
conditions with respect to the one dimensional spectrum.
is a Caratheodory function that satisfies certain
conditions with respect to the one dimensional spectrum.
Submitted January 23, 2006. Published May 19,2006.
Math Subject Classifications: 35J15, 35J70, 35J85.
Key Words: Boundary value problem; truncation; p-Laplacian; spectrum.
Show me the
PDF file (237K),
TEX file, and other files for this article.
 |
Aomar Anane
Departement de Mathematiques et Informatique
Faculte des Sciences
Universite Mohamed 1, Oujda, Maroc
email: anane@sciences.univ-oujda.ac.ma |
 |
Omar Chakrone
Departement de Mathematiques et Informatique
Faculte des Sciences
Universite Mohamed 1, Oujda, Maroc
email: chakrone@sciences.univ-oujda.ac.ma |
 |
Mohammed Chehabi
Departement de Mathematiques et Informatique
Faculte des Sciences
Universite Mohamed 1, Oujda, Maroc
email: chehb_md@yahoo.fr |
Return to the EJDE web page
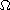 of
of
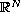 :
:
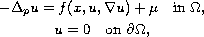
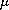 is a Radon measure on
is a Radon measure on
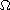 which is zero on
sets of
which is zero on
sets of
 -capacity zero,
-capacity zero,
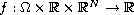 is a Caratheodory function that satisfies certain
conditions with respect to the one dimensional spectrum.
is a Caratheodory function that satisfies certain
conditions with respect to the one dimensional spectrum.


