Electron. J. Diff. Eqns.,
Vol. 2006(2006), No. 56, pp. 1-14.
Periodic solutions for some partial neutral functional
differential equations
Rachid Benkhalti, Abdelhai Elazzouzi, Khalil Ezzinbi
Abstract:
In this work, we study the existence of periodic solutions for
partial neutral functional differential equation.
We assume that the linear part is not necessarily densely defined
and satisfies the Hille-Yosida condition. In the nonhomogeneous
linear case, we prove that the existence of a bounded solution on
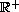 implies the existence of a periodic solution.
In nonlinear case, we use the concept of boundedness and ultimate
boundedness to prove the existence of periodic solutions.
implies the existence of a periodic solution.
In nonlinear case, we use the concept of boundedness and ultimate
boundedness to prove the existence of periodic solutions.
Submitted November 14, 2005. Published April 28, 2006.
Math Subject Classifications: 34C25, 34D40, 34K40, 34K60.
Key Words: Integral solutions; Hille-Yosida condition; boundedness;
ultimate boundedness; condensing map; Hale and Lunel's
fixed point theorem.
Show me the
PDF file (266K),
TEX file, and other files for this article.
 |
Rachid Benkhalti
Pacific Lutheran University, Department of Mathematics
Tacoma, Washington, 98447, USA
email: benkhar@plu.edu |
|---|
 |
Abdelhai Elazzouzi
Université Cadi Ayyad, Faculté des Sciences Semlalia
Département de Mathématiques, B.P. 2390 Marrakesh,
Morocco
email: a.elazzouzi@ucam.ac.ma
|
|---|
 |
Khalil Ezzinbi
Université Cadi Ayyad,
Faculté des Sciences Semlalia
Département de Mathématiques,
B.P. 2390 Marrakesh, Morocco
email: kezzinbi@ictp.it ezzinbi@ucam.ac.ma
|
|---|
Return to the EJDE web page
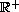 implies the existence of a periodic solution.
In nonlinear case, we use the concept of boundedness and ultimate
boundedness to prove the existence of periodic solutions.
implies the existence of a periodic solution.
In nonlinear case, we use the concept of boundedness and ultimate
boundedness to prove the existence of periodic solutions.


