Electron. J. Diff. Eqns.,
Vol. 2006(2006), No. 36, pp. 1-12.
Positive solutions for boundary-value problems of nonlinear
fractional differential equations
Shuqin Zhang
Abstract:
In this paper, we consider the existence and multiplicity
of positive solutions for the nonlinear fractional differential
equation boundary-value problem

where
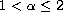 is a real number, and
is a real number, and
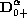 is the Caputo's fractional derivative,
and
is the Caputo's fractional derivative,
and
![$f:[0,1]\times[0,+\infty)\to [0,+\infty)$](gifs/ad.gif) is
continuous. By means of a fixed-point theorem on cones, some
existence and multiplicity results of positive solutions are
obtained.
is
continuous. By means of a fixed-point theorem on cones, some
existence and multiplicity results of positive solutions are
obtained.
Submitted November 30, 2005. Published March 21, 2006.
Math Subject Classifications: 34B15.
Key Words: Caputo's fractional derivative;
fractional differential equation; boundary-value problem;
positive solution; fractional Green's function; fixed-point theorem
An addendum as attached on November 9, 2009. It corrects the
definition of n in Lemmas 2.2 and 2.3. See the last page of this
article.
Show me the
PDF file (229K),
TEX file, and other files for this article.
 |
Shuqin Zhang
Department of Mathematics
University of Mining and Technology
Beijing, 100083 China
email: zhangshuqin@tsinghua.org.cn |
|---|
Return to the EJDE web page

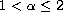 is a real number, and
is a real number, and
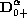 is the Caputo's fractional derivative,
and
is the Caputo's fractional derivative,
and
![$f:[0,1]\times[0,+\infty)\to [0,+\infty)$](gifs/ad.gif) is
continuous. By means of a fixed-point theorem on cones, some
existence and multiplicity results of positive solutions are
obtained.
is
continuous. By means of a fixed-point theorem on cones, some
existence and multiplicity results of positive solutions are
obtained.
