We prove the existence of solutions to the differential inclusion
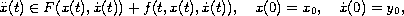
where
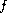 is a Caratheodory function and
is a Caratheodory function and
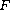 with nonconvex values in a Hilbert space such that
with nonconvex values in a Hilbert space such that
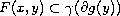 , with
, with
 a regular
locally Lipschitz function and
a regular
locally Lipschitz function and
 a linear operator.
a linear operator.
Tahar Haddad, Mustapha Yarou
Abstract:
We prove the existence of solutions to the differential
inclusion
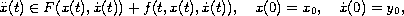
where
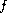 is a Caratheodory function and
is a Caratheodory function and
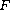 with nonconvex values in a Hilbert space such that
with nonconvex values in a Hilbert space such that
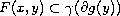 , with
, with
 a regular
locally Lipschitz function and
a regular
locally Lipschitz function and
 a linear operator.
a linear operator.
Submitted December 12, 2005. Published March 16, 2006.
Math Subject Classifications: 34A60, 49J52.
Key Words: Nonconvex differential inclusions; uniformly regular functions.
Show me the PDF file (212K), TEX file, and other files for this article.
 |
Tahar Haddad Department of Mathematics Faculty of Sciences, Jijel University, Algeria email: haddadtr2000@yahoo.fr |
|---|---|
 |
Mustapha Yarou Department of Mathematics Faculty of Sciences, Jijel University, Algeria email: mfyarou@yahoo.com |
Return to the EJDE web page