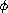 -Laplacian
-Laplacian
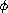 -Laplacian
-Laplacian
Vladimir Polasek, Irena Rachunkova
Abstract:
We investigate the singular periodic boundary-value problem
with
 -Laplacian,
-Laplacian,
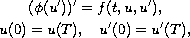
where
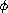 is an increasing homeomorphism,
is an increasing homeomorphism,
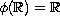 ,
,
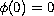 .
We assume that
.
We assume that
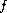 satisfies the Caratheodory conditions on
each set
satisfies the Caratheodory conditions on
each set
![$[a, b]\times \mathbb{R}^{2}$](gifs/ag.gif) ,
,
![$[a, b]\subset (0, T)$](gifs/ah.gif) and
and
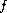 does not satisfy the Caratheodory conditions on
does not satisfy the Caratheodory conditions on
![$[0, T]\times \mathbb{R}^{2}$](gifs/ai.gif) , which means that
, which means that
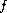 has time singularities at
has time singularities at
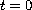 ,
,
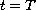 .
.
We provide sufficient conditions for the existence of solutions to
the above problem belonging to
![$C^{1}[0, T]$](gifs/al.gif) .
We also find conditions
which guarantee the existence of a sign-changing solution to the problem.
.
We also find conditions
which guarantee the existence of a sign-changing solution to the problem.
Submitted January 5, 2006. Published March 9, 2006.
Math Subject Classifications: 34B16, 34C25.
Key Words: Singular periodic problem;
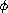 -Laplacian;
smooth sign-changing solutions; lower and upper functions.
-Laplacian;
smooth sign-changing solutions; lower and upper functions.
Show me the PDF file (269K), TEX file, and other files for this article.
 |
Vladimír Polásek Department of Mathematics, Palacky University Tomkova 40, 779 00 Olomouc, Czech Republic email: polasek.vlad@seznam.cz |
|---|---|
 |
Irena Rachunková Department of Mathematics, Palacky University Tomkova 40, 779 00 Olomouc, Czech Republic email: rachunko@inf.upol.cz |
Return to the EJDE web page