Electron. J. Diff. Eqns., Vol. 2006(2006), No. 16, pp. 1-19.
Inverse spectral analysis for singular
differential operators with matrix coefficients
Nour el Houda Mahmoud, Imen Yaich
Abstract:
Let
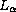 be the Bessel operator with
matrix coefficients defined on
be the Bessel operator with
matrix coefficients defined on
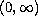 by
by
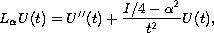
where
 is a fixed diagonal matrix. The aim of this study,
is to determine, on the positive half axis, a singular
second-order differential operator of
is a fixed diagonal matrix. The aim of this study,
is to determine, on the positive half axis, a singular
second-order differential operator of
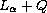 kind and its
various properties from only its spectral characteristics.
Here
kind and its
various properties from only its spectral characteristics.
Here
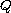 is a matrix-valued function. Under suitable
circumstances, the solution is constructed by means of the spectral
function, with the help of the Gelfund-Levitan process. The
hypothesis on the spectral function are inspired on the results
of some direct problems. Also the resolution of Fredholm's equations
and properties of Fourier-Bessel transforms are used here.
is a matrix-valued function. Under suitable
circumstances, the solution is constructed by means of the spectral
function, with the help of the Gelfund-Levitan process. The
hypothesis on the spectral function are inspired on the results
of some direct problems. Also the resolution of Fredholm's equations
and properties of Fourier-Bessel transforms are used here.
Submitted October 14, 2005. Published February 2, 2006.
Math Subject Classifications: 45Q05, 45B05, 45F15, 34A55, 35P99.
Key Words: Inverse problem; Fourier-Bessel transform;
spectral measure; Hilbert-Schmidt operator;
Fredholm's equation.
Show me the
PDF file (105K),
TEX file, and other files for this article.
Nour el Houda Mahmoud
Département de Mathématiques
Faculté des Sciences de Tunis
Campus Universitaire, 1060 Tunis, Tunisia
email: houda.mahmoud@fst.rnu.tn
|
Imen Yaïch
Département de Mathématiques
Faculté des Sciences de Tunis
Campus Universitaire, 1060 Tunis, Tunisia
email: imen.maalej@fst.rnu.tn
|
Return to the EJDE web page
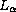 be the Bessel operator with
matrix coefficients defined on
be the Bessel operator with
matrix coefficients defined on
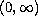 by
by
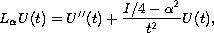
 is a fixed diagonal matrix. The aim of this study,
is to determine, on the positive half axis, a singular
second-order differential operator of
is a fixed diagonal matrix. The aim of this study,
is to determine, on the positive half axis, a singular
second-order differential operator of
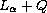 kind and its
various properties from only its spectral characteristics.
Here
kind and its
various properties from only its spectral characteristics.
Here
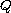 is a matrix-valued function. Under suitable
circumstances, the solution is constructed by means of the spectral
function, with the help of the Gelfund-Levitan process. The
hypothesis on the spectral function are inspired on the results
of some direct problems. Also the resolution of Fredholm's equations
and properties of Fourier-Bessel transforms are used here.
is a matrix-valued function. Under suitable
circumstances, the solution is constructed by means of the spectral
function, with the help of the Gelfund-Levitan process. The
hypothesis on the spectral function are inspired on the results
of some direct problems. Also the resolution of Fredholm's equations
and properties of Fourier-Bessel transforms are used here.