Using a reduced version of the sub and super-solutions method, we prove that the equation
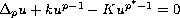 has a positive solution on a complete Riemannian manifold for
appropriate functions
has a positive solution on a complete Riemannian manifold for
appropriate functions
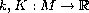 .
.
Mohammed Benalili, Youssef Maliki
Abstract:
Using a reduced version of the sub and super-solutions method,
we prove that the equation
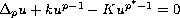 has a positive solution on a complete Riemannian manifold for
appropriate functions
has a positive solution on a complete Riemannian manifold for
appropriate functions
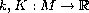 .
.
Submitted June 28, 2005. Published December 14, 2006.
Math Subject Classifications: 31C45, 53C21.
Key Words: Differential geometry; nonlinear partial
differential equations.
Show me the PDF file (203K), TEX file, and other files for this article.
 |
Mohammed Benalili Université Abou - Bekr Belkaïd Faculté des sciences Départ. Mthématiques B.P. 119, Tlemcen, Algerie email: m_benalili@mail.univ-tlemcen.dz |
|---|---|
 |
Youssef Maliki Université Abou - Bekr Belkaïd Faculté des sciences Départ. Mthématiques B.P. 119, Tlemcen, Algerie email: malyouc@yahoo.fr |
Return to the EJDE web page