Electron. J. Diff. Eqns.,
Vol. 2006(2006), No. 150, pp. 1-13.
Low regularity well-posedness for the one-dimensional
Dirac-Klein-Gordon system
Hartmut Pecher
Abstract:
Local well-posedness for Dirac-Klein-Gordon equations is proven in one
space dimension, where the Dirac part belongs to
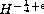 and
the Klein-Gordon part to
and
the Klein-Gordon part to
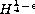 for
for
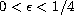 , and global well-posedness,
if the Dirac part belongs to the charge class
, and global well-posedness,
if the Dirac part belongs to the charge class
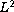 and the
Klein-Gordon part to
and the
Klein-Gordon part to
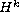 with
with
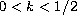 .
The proof uses a null structure in both nonlinearities detected
by d'Ancona, Foschi and Selberg and bilinear estimates in spaces
of Bourgain-Klainerman-Machedon type.
.
The proof uses a null structure in both nonlinearities detected
by d'Ancona, Foschi and Selberg and bilinear estimates in spaces
of Bourgain-Klainerman-Machedon type.
Submitted June 28, 2006. Published December 5, 2006.
Math Subject Classifications: 35Q40, 35L70.
Key Words: Dirac-Klein-Gordon system; well-posedness;
Fourier restriction norm method.
Show me the
PDF file (246K),
TEX file, and other files for this article.
Hartmut Pecher
Fachbereich Mathematik und Naturwissenschaften
Bergische Universitat Wuppertal
Gaustr. 20, D-42097 Wuppertal, Germany
email: Hartmut.Pecher@math.uni-wuppertal.de
|
Return to the EJDE web page
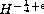 and
the Klein-Gordon part to
and
the Klein-Gordon part to
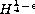 for
for
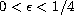 , and global well-posedness,
if the Dirac part belongs to the charge class
, and global well-posedness,
if the Dirac part belongs to the charge class
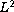 and the
Klein-Gordon part to
and the
Klein-Gordon part to
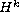 with
with
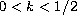 .
The proof uses a null structure in both nonlinearities detected
by d'Ancona, Foschi and Selberg and bilinear estimates in spaces
of Bourgain-Klainerman-Machedon type.
.
The proof uses a null structure in both nonlinearities detected
by d'Ancona, Foschi and Selberg and bilinear estimates in spaces
of Bourgain-Klainerman-Machedon type.