Electron. J. Diff. Eqns., Vol. 2006(2006), No. 141, pp. 1-12.
Periodic solutions for functional differential equations
with periodic delay close to zero
My Lhassan Hbid, Redouane Qesmi
Abstract:
This paper studies the existence of periodic solutions to the
delay differential equation
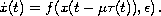
The analysis is based on a perturbation
method previously used for retarded differential equations with constant
delay. By transforming the studied equation into a perturbed non-autonomous
ordinary equation and using a bifurcation result and the Poincare
procedure for this last equation, we prove the existence of a branch
of periodic solutions, for the periodic delay equation, bifurcating
from
 .
.
Submitted August 25, 2006. Published November 9, 2006.
Math Subject Classifications: 34K13.
Key Words: Differential equation; periodic delay;
bifurcation; h-asymptotic stability; periodic solution.
Show me the
PDF file (232K),
TEX file, and other files for this article.
| |
My Lhassan Hbid
Département de Mathématiques, Faculté des Sciences Semlalia
Université Cadi Ayyad, B.P. S15, Marrakech, Morocco
email: hassan.hbid@gmail.com |
|---|
 |
Redouane Qesmi
Département de Mathématiques, Faculté des Sciences Semlalia
Université Cadi Ayyad, B.P. S15, Marrakech, Morocco
email: qesmir@gmail.com |
|---|
Return to the EJDE web page
 .
.
