Electron. J. Diff. Eqns.,
Vol. 2006(2006), No. 140, pp. 1-10.
Existence of periodic solution for perturbed
generalized Lienard equations
Islam Boussaada, A. Raouf Chouikha
Abstract:
Under conditions of Levinson-Smith type, we prove the existence
of a
 -periodic
solution for the perturbed generalized Lienard equation
-periodic
solution for the perturbed generalized Lienard equation
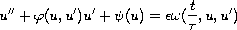
with periodic forcing term. Also we deduce sufficient condition for existence
of a periodic solution for the equation
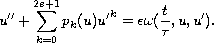
Our method can be applied also to the equation
![$$
u''+[u^2+(u+u')^2-1]u'+u=\epsilon\omega(\frac{t}{\tau},u,u').
$$](gifs/ad.gif)
The results obtained are illustrated with numerical examples.
Submitted May 15, 2006. Published November 1, 2006.
Math Subject Classifications: 34C25.
Key Words: Perturbed systems; Lienard equation; periodic solution.
Show me the
PDF file (567K),
TEX file, and other files for this article.
 |
Islam Boussaada
LMRS, UMR 6085, Universite de Rouen
Avenue de l'universit&aecute;e, BP.12
76801 Saint Etienne du Rouvray, France
email: islam.boussaada@etu.univ-rouen.fr
|
|---|
 |
A. Raouf Chouikha
Universite Paris 13 LAGA
Villetaneuse 93430, France
email: chouikha@math.univ-paris13.fr |
|---|
Return to the EJDE web page
 -periodic
solution for the perturbed generalized Lienard equation
-periodic
solution for the perturbed generalized Lienard equation
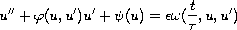
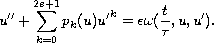
![$$
u''+[u^2+(u+u')^2-1]u'+u=\epsilon\omega(\frac{t}{\tau},u,u').
$$](gifs/ad.gif)

