Electron. J. Diff. Eqns.,
Vol. 2006(2006), No. 138, pp. 1-9.
The Dirichlet problem for the Monge-Ampere
equation in convex (but not strictly convex) domains
David Hartenstine
Abstract:
It is well-known that the Dirichlet problem for the Monge-Ampere
equation
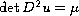 in a bounded strictly convex domain
in a bounded strictly convex domain
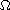 in
in
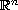 has a weak solution (in the sense of
Aleksandrov) for any finite Borel measure
has a weak solution (in the sense of
Aleksandrov) for any finite Borel measure
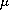 on
\Omega
and
for any continuous boundary data. We consider the Dirichlet
problem when
\Omega
is only assumed to be convex, and give a
necessary and sufficient condition on the boundary data for
solvability.
on
\Omega
and
for any continuous boundary data. We consider the Dirichlet
problem when
\Omega
is only assumed to be convex, and give a
necessary and sufficient condition on the boundary data for
solvability.
Submitted April 29, 2006. Published October 31, 2006.
Math Subject Classifications: 35J65, 35D05.
Key Words: Aleksandrov solutions; Perron method; viscosity solutions.
Show me the
PDF file (221K),
TEX file, and other files for this article.
 |
David Hartenstine
Department of Mathematics
Western Washington University
516 High Street, Bond Hall 202
Bellingham, WA 98225--9063, USA
email: david.hartenstine@wwu.edu
|
|---|
Return to the EJDE web page
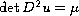 in a bounded strictly convex domain
in a bounded strictly convex domain
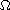 in
in
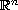 has a weak solution (in the sense of
Aleksandrov) for any finite Borel measure
has a weak solution (in the sense of
Aleksandrov) for any finite Borel measure
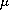 on
\Omega
and
for any continuous boundary data. We consider the Dirichlet
problem when
\Omega
is only assumed to be convex, and give a
necessary and sufficient condition on the boundary data for
solvability.
on
\Omega
and
for any continuous boundary data. We consider the Dirichlet
problem when
\Omega
is only assumed to be convex, and give a
necessary and sufficient condition on the boundary data for
solvability.
