Electron. J. Diff. Eqns.,
Vol. 2006(2006), No. 135, pp. 1-8.
Bifurcation of positive solutions for a semilinear equation
with critical Sobolev exponent
Yuanji Cheng
Abstract:
In this note we consider bifurcation of positive solutions to the
semilinear elliptic boundary-value problem with critical Sobolev
exponent
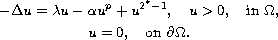
where
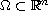 ,
,
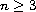 is a bounded
is a bounded
 -domain
-domain
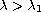 ,
,
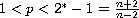 and
and
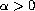 is a bifurcation parameter.
Brezis and Nirenberg [2] showed that a lower order (non-negative)
perturbation can contribute to regain the compactness and whence
yields existence of solutions. We study the equation with an
indefinite perturbation and prove a bifurcation result of two
solutions for this equation.
is a bifurcation parameter.
Brezis and Nirenberg [2] showed that a lower order (non-negative)
perturbation can contribute to regain the compactness and whence
yields existence of solutions. We study the equation with an
indefinite perturbation and prove a bifurcation result of two
solutions for this equation.
Submitted August 12, 2005. Published October 25, 2006.
Math Subject Classifications: 49K20, 35J65, 34B15.
Key Words: Critical Sobolev exponent; positive solutions; bifurcation.
Show me the
PDF file (232K),
TEX file, and other files for this article.
 |
Yuanji Cheng
School of Technology and Society
Malmo University
SE-205 06 Malmo, Sweden
email: yuanji.cheng@ts.mah.se |
|---|
Return to the EJDE web page
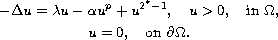
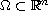 ,
,
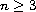 is a bounded
is a bounded
 -domain
-domain
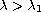 ,
,
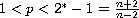 and
and
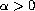 is a bifurcation parameter.
Brezis and Nirenberg [2] showed that a lower order (non-negative)
perturbation can contribute to regain the compactness and whence
yields existence of solutions. We study the equation with an
indefinite perturbation and prove a bifurcation result of two
solutions for this equation.
is a bifurcation parameter.
Brezis and Nirenberg [2] showed that a lower order (non-negative)
perturbation can contribute to regain the compactness and whence
yields existence of solutions. We study the equation with an
indefinite perturbation and prove a bifurcation result of two
solutions for this equation.
