Electron. J. Diff. Eqns.,
Vol. 2006(2006), No. 131, pp. 1-15.
A semilinear elliptic problem involving nonlinear boundary
condition and sign-changing potential
Tsung-fang Wu
Abstract:
In this paper, we study the multiplicity of nontrivial nonnegative
solutions for a semilinear elliptic equation involving nonlinear
boundary condition and sign-changing potential. With the help of
the Nehari manifold, we prove that the semilinear elliptic
equation:
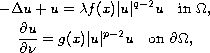
has at least two nontrivial nonnegative solutions for
 is sufficiently small.
is sufficiently small.
Submitted July 6, 2006. Published October 17, 2006.
Math Subject Classifications: 35J65, 35J50, 35J55.
Key Words: Semilinear elliptic equations; Nehari manifold;
Nonlinear boundary condition.
Show me the
PDF file (255K),
TEX file, and other files for this article.
 |
Tsung-Fang Wu
Department of Applied Mathematics
National University of Kaohsiung
Kaohsiung 811, Taiwan
email: tfwu@nuk.edu.tw |
|---|
Return to the EJDE web page
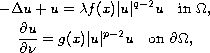
 is sufficiently small.
is sufficiently small.
