Electron. J. Diff. Eqns.,
Vol. 2006(2006), No. 124, pp. 1-12.
Convexity of level sets for solutions to nonlinear elliptic
problems in convex rings
Paola Cuoghi, Paolo Salani
Abstract:
We find suitable assumptions for the quasi-concave
envelope
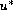 of a solution (or a subsolution)
of a solution (or a subsolution)
 of an elliptic
equation
of an elliptic
equation
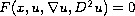 (possibly fully nonlinear)
to be a viscosity subsolution of the same equation.
We apply this result to study the convexity of level sets of
solutions to elliptic Dirichlet problems in a convex ring
(possibly fully nonlinear)
to be a viscosity subsolution of the same equation.
We apply this result to study the convexity of level sets of
solutions to elliptic Dirichlet problems in a convex ring
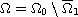 .
.
Submitted June 23, 2005. Published October 11, 2006.
Math Subject Classifications: 35J25, 35J65.
Key Words: Elliptic equations; convexity of level sets;
quasi-concave envelope.
Show me the
PDF file (243K),
TEX file, and other files for this article.
 |
Paola Cuoghi
Dipt. di Matematica Pura e Applicata
Universitá degli Studi di Modena e Reggio Emilia
via Campi 213/B, 41100 Modena -Italy
email: pcuoghi@unimo.it |
|---|
 |
Paolo Salani
Dipt. di Matematica "U. Dini"
viale Morgagni 67/A, 50134 Firenze, Italy
email: salani@math.unifi.it |
|---|
Return to the EJDE web page
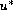 of a solution (or a subsolution)
of a solution (or a subsolution)
 of an elliptic
equation
of an elliptic
equation
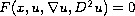 (possibly fully nonlinear)
to be a viscosity subsolution of the same equation.
We apply this result to study the convexity of level sets of
solutions to elliptic Dirichlet problems in a convex ring
(possibly fully nonlinear)
to be a viscosity subsolution of the same equation.
We apply this result to study the convexity of level sets of
solutions to elliptic Dirichlet problems in a convex ring
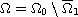 .
.

