Electron. J. Diff. Eqns.,
Vol. 2006(2006), No. 102, pp. 1-9.
Existence of positive solutions for higher order singular
sublinear elliptic equations
Imed Bachar
Abstract:
We present existence result for the polyharmonic nonlinear
problem
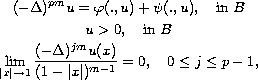
in the sense of distributions.
Here
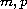 are positive integers,
are positive integers,
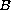 is the unit ball in
is the unit ball in
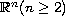 and the nonlinearity is a sum of a singular and
sublinear terms satisfying some appropriate conditions related to a
polyharmonic Kato class of functions
and the nonlinearity is a sum of a singular and
sublinear terms satisfying some appropriate conditions related to a
polyharmonic Kato class of functions
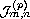 .
.
Submitted May 10, 2006. Published August 31, 2006.
Math Subject Classifications: 34B27, 35J40.
Key Words: Green function; higher-order elliptic equations;
positive solution; Schauder fixed point theorem.
Show me the
PDF file (238K),
TEX file, and other files for this article.
 |
Imed Bachar
Département de mathématiques
Faculté des sciences de Tunis
campus universitaire, 2092 Tunis, Tunisia
email: Imed.Bachar@ipeit.rnu.tn |
|---|
Return to the EJDE web page
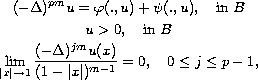
 are positive integers,
are positive integers,
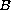 is the unit ball in
is the unit ball in
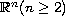 and the nonlinearity is a sum of a singular and
sublinear terms satisfying some appropriate conditions related to a
polyharmonic Kato class of functions
and the nonlinearity is a sum of a singular and
sublinear terms satisfying some appropriate conditions related to a
polyharmonic Kato class of functions
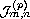 .
.
