In this paper we show that the scale of Sobolev-Campanato spaces
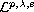 contain the general
BMO-Triebel-Lizorkin spaces
contain the general
BMO-Triebel-Lizorkin spaces
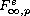 as special cases,
so that the conjecture by Triebel regarding estimates for
solutions of scalar regular elliptic boundary value problems in
as special cases,
so that the conjecture by Triebel regarding estimates for
solutions of scalar regular elliptic boundary value problems in
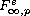 spaces (solved in the case
spaces (solved in the case
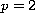 in a previous
work) is completely solved now.
Also we prove that the method used for the scalar case works
for systems, and we give a priori estimates near the boundary for
solutions of regular elliptic systems in the general spaces
in a previous
work) is completely solved now.
Also we prove that the method used for the scalar case works
for systems, and we give a priori estimates near the boundary for
solutions of regular elliptic systems in the general spaces
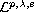 containing BMO,
containing BMO,
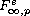 ,
and Morrey-Campanato spaces
,
and Morrey-Campanato spaces
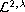 as special cases. This result extends the work by the author
in the scalar case.
as special cases. This result extends the work by the author
in the scalar case.
