Electron. J. Diff. Eqns., Vol. 2005(2005), No. 90, pp. 1-18.

Half-linear dynamic equations with mixed derivatives

Ondrej Dosly, Daniel Marek

Abstract:
We investigate oscillatory properties of the second order half-linear dynamic equation on a time scale with mixed derivatives
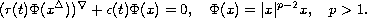
$$ (r(t)\Phi(x^{\Delta}))^\nabla+c(t)\Phi(x)=0,\quad \Phi(x)=|x|^{p-2}x, \quad p>1. $$
In particular, we establish the Roundabout theorem which relates oscillatory properties of this equation to the solvability of the associated Riccati-type dynamic equation and to the positivity of the corresponding energy functional. This result is then used to prove (non)oscillation criteria for the above equation.

Submitted March 17, 2005. Published August 15, 2005.
Math Subject Classifications: 39A10.
Key Words: Time scale; half-linear dynamic equations; mixed derivatives; Picone's identity; roundabout theorem.

Show me the PDF file (258K), TEX file, and other files for this article.

Ondrej Dosly
Department of Mathematics
Masaryk University, Janackovo nam. 2a
CZ-662 95 Brno, Czech Republic
email: dosly@math.muni.cz
Daniel Marek
Department of Mathematics
Masaryk University, Janackovo nam. 2a
CZ-662 95 Brno, Czech Republic
email: marek275@math.muni.cz

Return to the EJDE web page