Electron. J. Diff. Eqns.,
Vol. 2005(2005), No. 76, pp. 1-13.
Oscillation of second-order nonlinear differential equations
with a damping term
Elmetwally M. Elabbasy, Taher S. Hassan, Samir. H. Saker
Abstract:
This paper concerns the oscillation of solutions to the differential equation
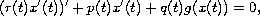
where
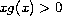 for all
for all
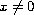 ,
,
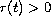 for
for
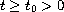 . No sign conditions are imposed on
. No sign conditions are imposed on
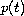 and
and
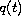 .
Our results solve the open problem posed by Rogovchenko [27],
complement the results in Sun [29], and improve a number of existing
oscillation criteria. Our main results are illustrated with examples.
.
Our results solve the open problem posed by Rogovchenko [27],
complement the results in Sun [29], and improve a number of existing
oscillation criteria. Our main results are illustrated with examples.
Submitted April 5, 2005. Published July 8, 2005.
Math Subject Classifications: 34K15, 34C10.
Key Words: Oscillation; second order nonlinear differential equation;
damping term.
Acorrigendum was posted on January 2, 2008. A new assumption is included
in Theorems 2.2 and 2.4, and Example 2.3 is modified. Please see the last
page of this manuscript.
Show me the
PDF file (252K),
TEX file, and other files for this article.
 |
Elmetwally M. Elabbasy
Department of Mathematics
Faculty of Science,
Mansoura University
Mansoura, 35516, Egypt
email: emelabbasy@mans.edu.eg
|
|---|
 |
Taher S. Hassan
Department of Mathematics
Faculty of Science,
Mansoura University
Mansoura, 35516, Egypt
email: tshassan@mans.edu.eg
|
|---|
 |
Samir H. Saker
Department of Mathematics
Faculty of Science,
Mansoura University
Mansoura, 35516, Egypt
email: shsaker@mans.edu.eg
|
|---|
Return to the EJDE web page
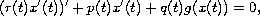
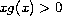 for all
for all
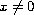 ,
,
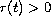 for
for
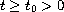 . No sign conditions are imposed on
. No sign conditions are imposed on
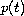 and
and
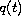 .
Our results solve the open problem posed by Rogovchenko [27],
complement the results in Sun [29], and improve a number of existing
oscillation criteria. Our main results are illustrated with examples.
.
Our results solve the open problem posed by Rogovchenko [27],
complement the results in Sun [29], and improve a number of existing
oscillation criteria. Our main results are illustrated with examples.


