In [7] and [8], Parker and Sochacki considered iterative methods for computing the power series solution to
where
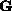is a polynomial
from
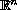to
,
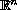including truncations of
Picard iteration. The authors demonstrated that many ODE's may be
transformed into computationally feasible polynomial problems of this
type, and the methods generalize to a broad class of initial value PDE's.
In this paper we show that the subset of the real analytic functions
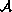consisting of functions that are components of the solution
to polynomial differential equations is a proper subset of
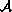and
that it shares the field and near-field structure of
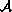, thus
making it a proper sub-algebra. Consequences of the algebraic structure
are investigated.
Using these results we show that the Maclaurin or Taylor series can be
generated algebraically for a large class of functions. This finding
can be used to generate efficient numerical methods of arbitrary order
(accuracy) for initial value ordinary differential equations.
Examples to indicate these techniques are presented. Future advances
in numerical solutions to initial value ordinary differential equations
are indicated.
