In this paper, we investigate the boundary between existence and nonexistence for positive solutions of Dirichlet problem
,
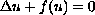where
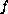has supercritical growth.
Pohozaev showed that for convex or polar domains, no positive
solutions may be found. Ding and others showed that for domains with
non-trivial topology, there are examples of existence of positive
solutions. The goal of this paper is to illuminate the transition
from non-existence to existence of solutions for the nonlinear
eigenvalue problem as the domain moves from simple (convex) to complex
(non-trivial topology).
To this end, we present the construction of several domains in
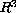which are not starlike (polar) but still admit a Pohozaev nonexistence
argument for a general class of nonlinearities. One such domain is a
long thin tubular domain which is curved and twisted in space. It
presents complicated geometry, but simple topology. The construction
(and the lemmas leading to it) are new and combined with established
theorems narrow the gap between non-existence and existence
strengthening the notion that trivial domain topology is the
ingredient for non-existence.
