Electron. J. Diff. Eqns., Vol. 2005(2005), No. 23, pp. 1-7.
Extinction for fast diffusion equations with
nonlinear sources
Yuxiang Li, Jichun Wu
Abstract:
We establish conditions for the extinction of solutions,
in finite time, of the fast diffusion problem
 ,
,
 ,
in a bounded domain of
,
in a bounded domain of
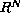 with
with
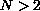 .
More precisely, we show that if
.
More precisely, we show that if
 ,
the solution with small initial data vanishes in finite time,
and if
,
the solution with small initial data vanishes in finite time,
and if  , the maximal solution is positive for all
, the maximal solution is positive for all
 .
If
.
If
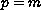 ,
then first eigenvalue of the Dirichlet problem plays
a role.
,
then first eigenvalue of the Dirichlet problem plays
a role.
Submitted September 15, 2004. Published February 20, 2005.
Math Subject Classifications: 35K20, 35K55.
Key Words: Extinction; fast diffusion; first eigenvalue.
Show me the
PDF file (198K),
TEX file, and other files for this article.
 |
Yuxiang Li
Department of Mathematics, Southeast University
Nanjing 210096, China.
Department of Earth Sciences,
Nanjing University
Nanjing 210093, China
email: lieyuxiang@yahoo.com.cn |
|---|
| |
Jichun Wu
Department of Earth Sciences,
Nanjing University
Nanjing 210093, China
email: jcwu@nju.edu.cn |
|---|
Return to the EJDE web page
 ,
,
 ,
in a bounded domain of
,
in a bounded domain of
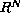 with
with
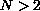 .
More precisely, we show that if
.
More precisely, we show that if
 ,
the solution with small initial data vanishes in finite time,
and if
,
the solution with small initial data vanishes in finite time,
and if  , the maximal solution is positive for all
, the maximal solution is positive for all
 .
If
.
If
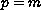 ,
then first eigenvalue of the Dirichlet problem plays
a role.
,
then first eigenvalue of the Dirichlet problem plays
a role.
