Electron. J. Diff. Eqns., Vol. 2005(2005), No. 146, pp. 1-14.

Multiplicity and symmetry breaking for positive radial solutions of semilinear elliptic equations modelling MEMS on annular domains

Peng Feng, Zhengfang Zhou

Abstract:
The use of electrostatic forces to provide actuation is a method of central importance in microelectromechanical system (MEMS) and in nanoelectromechanical systems (NEMS). Here, we study the electrostatic deflection of an annular elastic membrane. We investigate the exact number of positive radial solutions and non-radially symmetric bifurcation for the model
$$ -\Delta u=\frac{\lambda}{(1-u)^2}\quad\hbox{in }\Omega, \quad u=0 \quad\hbox{on }\partial \Omega, $$
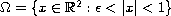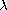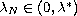where $\Omega=\{x\in \mathbb{R}^2: \epsilon<|x| less than 1\}$. The exact number of positive radial solutions maybe 0, 1, or 2 depending on $\lambda$. It will be shown that the upper branch of radial solutions has non-radially symmetric bifurcation at infinitely many $\lambda_N\in (0,\lambda^*)$. The proof of the multiplicity result relies on the characterization of the shape of the time-map. The proof of the bifurcation result relies on a well-known theorem due to Kielhofer.

Submitted August 10, 2005. Published December 12, 2005.
Math Subject Classifications: 35J65, 35J60, 35B32.
Key Words: Radial solution; symmetry breaking; multiplicity; MEMS.

Show me the PDF file (295K), TEX file, and other files for this article.

Peng Feng
Department of Mathematics
Michigan State University
East Lansing, MI 48824, USA
email: fengpeng@math.msu.edu
Zhengfang Zhou
Department of Mathematics
Michigan State University
East Lansing, MI 48824, USA
email: zfzhou@math.msu.edu

Return to the EJDE web page