Electron. J. Diff. Eqns., Vol. 2005(2005), No. 142, pp. 1-11.

Periodicity and stability in neutral nonlinear differential equations with functional delay

Youssef M. Dib, Mariette R. Maroun, Youssef N. Raffoul

Abstract:
We study the existence and uniqueness of periodic solutions and the stability of the zero solution of the nonlinear neutral differential equation
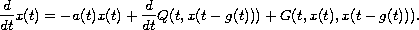
$$ \frac{d}{dt}x(t) = -a(t)x(t)+ \frac{d}{dt}Q(t, x(t-g(t))) +G(t,x(t), x(t-g(t))). $$
In the process we use integrating factors and convert the given neutral differential equation into an equivalent integral equation. Then we construct appropriate mappings and employ Krasnoselskii's fixed point theorem to show the existence of a periodic solution of this neutral differential equation. 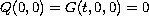We also use the contraction mapping principle to show the existence of a unique periodic solution and the asymptotic stability of the zero solution provided that $Q(0,0)= G(t, 0,0) = 0$.

Submitted November 30, 2004. Published December 6, 2005.
Math Subject Classifications: 34K20, 45J05, 45D05.
Key Words: Krasnoselskii; contraction; neutral differential equation; integral equation; periodic solution; asymptotic stability

Show me the PDF file (241K), TEX file, and other files for this article.

  Youssef M. Dib
Department of Mathematics, University of Louisiana
Lafayette, LA 70504-1010, USA
email: youssef@louisiana.edu
  Mariette R. Maroun
Department of Mathematics, Baylor University
Waco, TX 76798-7328, USA
email: Mariette_Maroun@baylor.edu
Youssef N. Raffoul
Department of Mathematics, University of Dayton
Dayton, OH 45469-2316, USA
e-mail: youssef.raffoul@notes.udayton.edu

Return to the EJDE web page