Electron. J. Diff. Eqns., Vol. 2005(2005), No. 139, pp. 1-15.

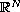
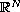
Existence and uniqueness of positive solutions to a quasilinear elliptic problem in $\mathbb{R}^{N}$

Dragos-Patru Covei

Abstract:
We prove the existence of a unique positive solution to the problem
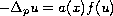
$$ -\Delta _{p}u=a(x)f(u) $$
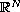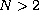in $\mathbb{R}^{N}$, $N>2$. Our result extended previous works by Cirstea-Radulescu and Dinu, while the proofs are based on two theorems on bounded domains, due to Diaz-Saa and Goncalves-Santos.

Submitted June 8, 2005. Published December 5, 2005.
Math Subject Classifications: 35J60, 35J70.
Key Words: Quasilinear elliptic problem; uniqueness; existence; nonexistence; lower-upper solutions.

A corrigendum was posted on October 8, 2007. Some misprints are corrected and the existence of solutions is clarified. Please see the last page of this manuscript.

Show me the PDF file (245K), TEX file, and other files for this article.

Dragos-Patru Covei
Constantin Brancusi' University of Targu-Jiu
Bulevardul Republicii, nr. 1
210152 Targu-Jiu, Romania
email: dragoscovei77@yahoo.com

Return to the EJDE web page