In this paper we consider the existence of nonzero solutions for the undecoupling elliptic system
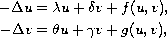
on a bounded domain of
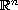 ,
with zero Dirichlet boundary
conditions. We use the Lyapunov-Schmidt method and the fixed-point
principle.
,
with zero Dirichlet boundary
conditions. We use the Lyapunov-Schmidt method and the fixed-point
principle.
Quoc Anh Ngo
Abstract:
In this paper we consider the existence of nonzero solutions for
the undecoupling elliptic system
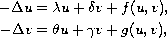
on a bounded domain of
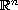 ,
with zero Dirichlet boundary
conditions. We use the Lyapunov-Schmidt method and the fixed-point
principle.
,
with zero Dirichlet boundary
conditions. We use the Lyapunov-Schmidt method and the fixed-point
principle.
Submitted July 12, 2005. Published November 23, 2005.
Math Subject Classifications: 35J50, 35J55.
Key Words: Semilinear; elliptic system; Lyapunov; Schmidt;
fixed-point principle.
Show me the PDF file (222K), TEX file, and other files for this article.
 |
Quoc Anh Ngo Department of Mathematics, Mechanics and Informatics College of Science, Vietnam National University Hanoi, Vietnam email: bookworm_vn@yahoo.com anhngq@yahoo.com.vn |
|---|
Return to the EJDE web page