Electron. J. Diff. Eqns., Vol. 2005(2005), No. 127, pp. 1-7.

Eigenvalues and symmetric positive solutions for a three-point boundary-value problem

Yongping Sun

Abstract:
In this paper, we consider the second-order three-point boundary-value problem
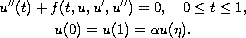
$$\displaylines{ u''(t)+f(t,u,u',u'')=0,\quad 0\leq t\leq 1,\cr u(0)=u(1)=\alpha u(\eta). }$$
Under suitable conditions and using Schauder fixed point theorem, we prove the existence of at least one symmetric positive solution. We also study the existence of positive eigenvalues for this problem. We emphasis the highest-order derivative occurs nonlinearly in our problem.

Submitted September 15, 2005. Published November 23, 2005.
Math Subject Classifications: 34B10, 34B15.
Key Words: Symmetric positive solution; three-point boundary-value problem; Schauder fixed point theorem; eigenvalue.

Show me the PDF file (177K), TEX file, and other files for this article.

Yongping Sun
Department of Fundamental Courses
Hangzhou Radio & TV University
Hangzhou, Zhejiang 310012, China
email: sunyongping@126.com

Return to the EJDE web page