Electron. J. Diff. Eqns.,
Vol. 2005(2005), No. 116, pp. 1-43.
Pseudodifferential operators with generalized symbols
and regularity theory
Claudia Garetto, Todor Gramchev, Michael Oberguggenberger
Abstract:
We study pseudodifferential operators with amplitudes
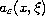 depending on a singular parameter
depending on a singular parameter
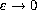 with asymptotic properties measured by different
scales. We prove, taking into account the asymptotic behavior
for
with asymptotic properties measured by different
scales. We prove, taking into account the asymptotic behavior
for
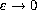 ,
refined versions of estimates for classical
pseudodifferential operators. We apply these estimates to nets of
regularizations of exotic operators as well as operators with amplitudes
of low regularity, providing a unified method for treating both classes.
Further, we develop a full symbolic calculus for pseudodifferential
operators acting on algebras of Colombeau generalized functions.
As an application, we formulate a sufficient condition of hypoellipticity
in this setting, which leads to regularity results for generalized
pseudodifferential equations.
,
refined versions of estimates for classical
pseudodifferential operators. We apply these estimates to nets of
regularizations of exotic operators as well as operators with amplitudes
of low regularity, providing a unified method for treating both classes.
Further, we develop a full symbolic calculus for pseudodifferential
operators acting on algebras of Colombeau generalized functions.
As an application, we formulate a sufficient condition of hypoellipticity
in this setting, which leads to regularity results for generalized
pseudodifferential equations.
Submitted June 13, 2005. Published October 21, 2005.
Math Subject Classifications: 35S50, 35S30, 46F10, 46F30, 35D10.
Key Words: Pseudodifferential operators; small parameter;
slow scale net; algebras of generalized functions.
Show me the
PDF file (524K),
TEX file, and other files for this article.
 |
Claudia Garetto
Institut für Technische Mathematik
Geometrie und Bauinformatik
Universität Innsbruck
A - 6020 Innsbruck, Austria
email: claudia@mat1.uibk.ac.at |
|---|
 |
Todor Gramchev
Dipartimento di Matematica e Informatica
Universitá di Cagliari, I - 09124 Cagliari, Italia
email: todor@unica.it |
|---|
 |
Michael Oberguggenberger
Institut für Technische Mathematik
Geometrie und Bauinformatik
Universität Innsbruck
A - 6020 Innsbruck, Austria
email: michael@mat1.uibk.ac.at |
|---|
Return to the EJDE web page
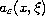 depending on a singular parameter
depending on a singular parameter
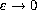 with asymptotic properties measured by different
scales. We prove, taking into account the asymptotic behavior
for
with asymptotic properties measured by different
scales. We prove, taking into account the asymptotic behavior
for
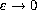 ,
refined versions of estimates for classical
pseudodifferential operators. We apply these estimates to nets of
regularizations of exotic operators as well as operators with amplitudes
of low regularity, providing a unified method for treating both classes.
Further, we develop a full symbolic calculus for pseudodifferential
operators acting on algebras of Colombeau generalized functions.
As an application, we formulate a sufficient condition of hypoellipticity
in this setting, which leads to regularity results for generalized
pseudodifferential equations.
,
refined versions of estimates for classical
pseudodifferential operators. We apply these estimates to nets of
regularizations of exotic operators as well as operators with amplitudes
of low regularity, providing a unified method for treating both classes.
Further, we develop a full symbolic calculus for pseudodifferential
operators acting on algebras of Colombeau generalized functions.
As an application, we formulate a sufficient condition of hypoellipticity
in this setting, which leads to regularity results for generalized
pseudodifferential equations.


