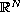
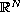
Gustavo Izquierdo B., Gabriel Lopez G.
Abstract:
We show the existence of a weak solution for the problem
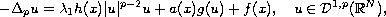
where,
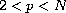 ,
,
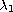 is the first eigenvalue of the
is the first eigenvalue of the
 -Laplacian on
-Laplacian on
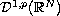 relative to
the radially symmetric weight
relative to
the radially symmetric weight
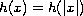 .
In this problem,
.
In this problem,
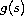 is a bounded function for all
is a bounded function for all
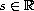 ,
,
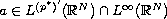 and
and
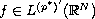 . To establish an existence result,
we employ the Saddle Point Theorem of Rabinowitz [9] and an
improved Poincare inequality from an article of Alziary,
Fleckinger and Takac [2].
. To establish an existence result,
we employ the Saddle Point Theorem of Rabinowitz [9] and an
improved Poincare inequality from an article of Alziary,
Fleckinger and Takac [2].
Submitted May 31, 2005. Published October 17, 2005.
Math Subject Classifications: 35J20.
Key Words: Resonance; p-Laplacian; improved Poincare inequality
Show me the PDF file (218K), TEX file, and other files for this article.
 |
Gustavo Izquierdo Buenrostro Dept. Mat. Universidad Autonoma Metropolitana Mexico email: iubg@xanum.uam.mx |
|---|---|
 |
Gabriel Lopez Garza
Dept. Mat. Universidad Autonoma Metropolitana Mexico email: grlzgz@xanum.uam.mx |
Return to the EJDE web page