Electron. J. Diff. Eqns.,
Vol. 2005(2005), No. 111, pp. 1-8.
Existence and uniqueness of mild and classical solutions of
impulsive evolution equations
Annamalai Anguraj, Mani Mallika Arjunan
Abstract:
We consider the non-linear impulsive evolution equation
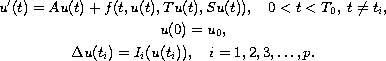
in a Banach space
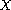 , where
, where
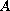 is the infinitesimal generator
of a
is the infinitesimal generator
of a
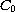 semigroup. We study the existence
and uniqueness of the mild solutions of the evolution equation
by using semigroup theory and then show that the mild solutions
give rise to a classical solutions.
semigroup. We study the existence
and uniqueness of the mild solutions of the evolution equation
by using semigroup theory and then show that the mild solutions
give rise to a classical solutions.
Submitted June 15, 2005. Published October 17, 2005.
Math Subject Classifications: 34A37, 34G60, 34G20.
Key Words: Semigroups; evolution equations; impulsive conditions.
Show me the
PDF file (180K),
TEX file, and other files for this article.
 |
Annamalai Anguraj
Department of Mathematics
P.S.G. College of Arts and Science
Coimbatore - 641 014, Tamilnadu, India
email: angurajpsg@yahoo.com |
|---|
 |
Mani Mallika Arjunan
Department of Mathematics
P.S.G. College of Arts and Science
Coimbatore- 641 014, Tamilnadu, India
email: arjunphd07@yahoo.co.in |
|---|
Return to the EJDE web page
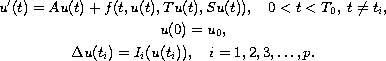
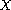 , where
, where
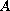 is the infinitesimal generator
of a
is the infinitesimal generator
of a
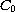 semigroup. We study the existence
and uniqueness of the mild solutions of the evolution equation
by using semigroup theory and then show that the mild solutions
give rise to a classical solutions.
semigroup. We study the existence
and uniqueness of the mild solutions of the evolution equation
by using semigroup theory and then show that the mild solutions
give rise to a classical solutions.

