A classical result of Aleksandrov allows us to estimate the size of a convex function
 at a point
at a point
 in a bounded domain
in a bounded domain
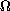 in terms of the distance from
in terms of the distance from
 to the boundary of
to the boundary of
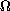 if
if
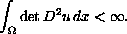
This estimate plays a prominent role in the existence and regularity theory of the Monge-Ampere equation. Jerison proved an extension of Aleksandrov's result that provides a similar estimate, in some cases for which this integral is infinite. Gutierrez and Huang proved a variant of the Aleksandrov estimate, relevant to solutions of a parabolic Monge-Ampere equation. In this paper, we prove Jerison-like extensions to this parabolic estimate.
