Electron. J. Diff. Eqns.,
Vol. 2004(2004), No. 90, pp. 1-24.
Partial compactness for the 2-D Landau-Lifshitz flow
Paul Harpes
Abstract:
Uniform local
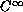 -bounds
for Ginzburg-Landau type
approximations for the Landau-Lifshitz flow on planar domains
are proven. They hold outside an energy-concentration set of
locally finite parabolic Hausdorff-dimension 2, which has
finite times-slices. The approximations subconverge to a global
weak solution of the Landau-Lifshitz flow, which is smooth away
from the energy concentration set. The same results hold for
sequences of global smooth solutions of the 2-d Landau-Lifshitz flow.
-bounds
for Ginzburg-Landau type
approximations for the Landau-Lifshitz flow on planar domains
are proven. They hold outside an energy-concentration set of
locally finite parabolic Hausdorff-dimension 2, which has
finite times-slices. The approximations subconverge to a global
weak solution of the Landau-Lifshitz flow, which is smooth away
from the energy concentration set. The same results hold for
sequences of global smooth solutions of the 2-d Landau-Lifshitz flow.
Submitted September 11, 2003. Published July 5, 2004.
Math Subject Classifications: 35B65, 35B45, 35D05, 35D10, 35K45, 35K50, 35K55.
Key Words: Partial compactness; partial regularity;
Landau-Lifshitz flow; a priori estimates; harmonic map flow;
non-linear parabolic; Struwe-solution; approximations.
Show me the
PDF file (364K),
TEX file, and other files for this article.
 |
Paul Harpes
ETH Zurich
Ramistrasse 101, 8092 Zurich, Switzerland
email: pharpes@math.ethz.ch |
|---|
Return to the EJDE web page
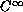 -bounds
for Ginzburg-Landau type
approximations for the Landau-Lifshitz flow on planar domains
are proven. They hold outside an energy-concentration set of
locally finite parabolic Hausdorff-dimension 2, which has
finite times-slices. The approximations subconverge to a global
weak solution of the Landau-Lifshitz flow, which is smooth away
from the energy concentration set. The same results hold for
sequences of global smooth solutions of the 2-d Landau-Lifshitz flow.
-bounds
for Ginzburg-Landau type
approximations for the Landau-Lifshitz flow on planar domains
are proven. They hold outside an energy-concentration set of
locally finite parabolic Hausdorff-dimension 2, which has
finite times-slices. The approximations subconverge to a global
weak solution of the Landau-Lifshitz flow, which is smooth away
from the energy concentration set. The same results hold for
sequences of global smooth solutions of the 2-d Landau-Lifshitz flow.
